Elettricità
Cariche, campi, potenziale e corrente
L'ambra e l'idea di carica elettrica
- Osserviamo un'interazione a distanza, senza necessità di contatto
- L'interazione può essere sia attrattiva sia repulsiva
- La stessa azione su oggetti diversi genera effetti diversi
L'elettroscopio di Volta
Cariche, isolanti e conduttori
Conduttori ed isolanti
Metalli

Isolanti

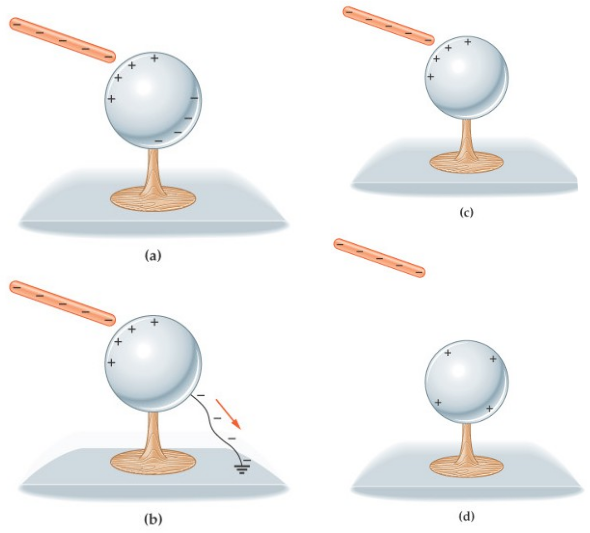
Carica per induzione di un conduttore
Legge di Coulomb
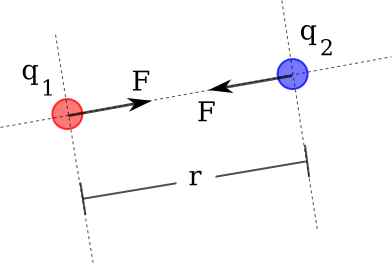
\[ F_{\mathrm{el}} = k \frac{q_{1}q_{2}}{r^{2}}; \; k = \frac{1}{4 \pi \varepsilon_{0}} \]
\[ F_{\mathrm{el}} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{1}q_{2}}{r^{2}} \]
\[ q \Rightarrow Coulomb \, [C] \]
\[ e = 1.6 \cdot 10^{-19} (C) \]
Campo elettrico
\[ \vec{F}_{\mathrm{el}} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{0}q}{r^{2}} \vec{u}_{r} \]
\[ \vec{E} = \frac{\vec{F}_{\mathrm{el}}}{q_{0}} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{r^{2}} \vec{u}_{r} \]
Linee di forza del campo elettrico: 1
Dipolo elettrico
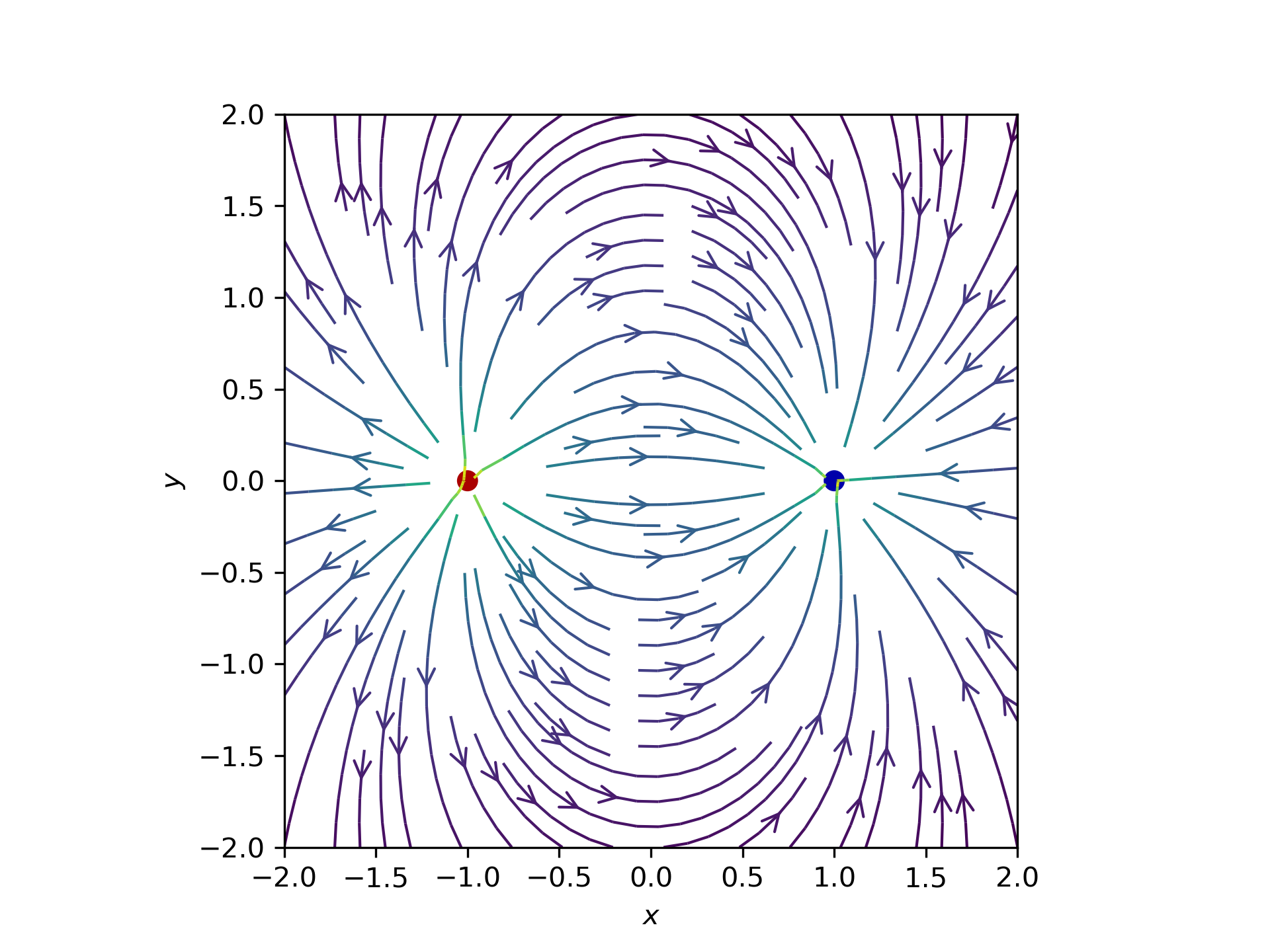
Quadrupolo elettrico
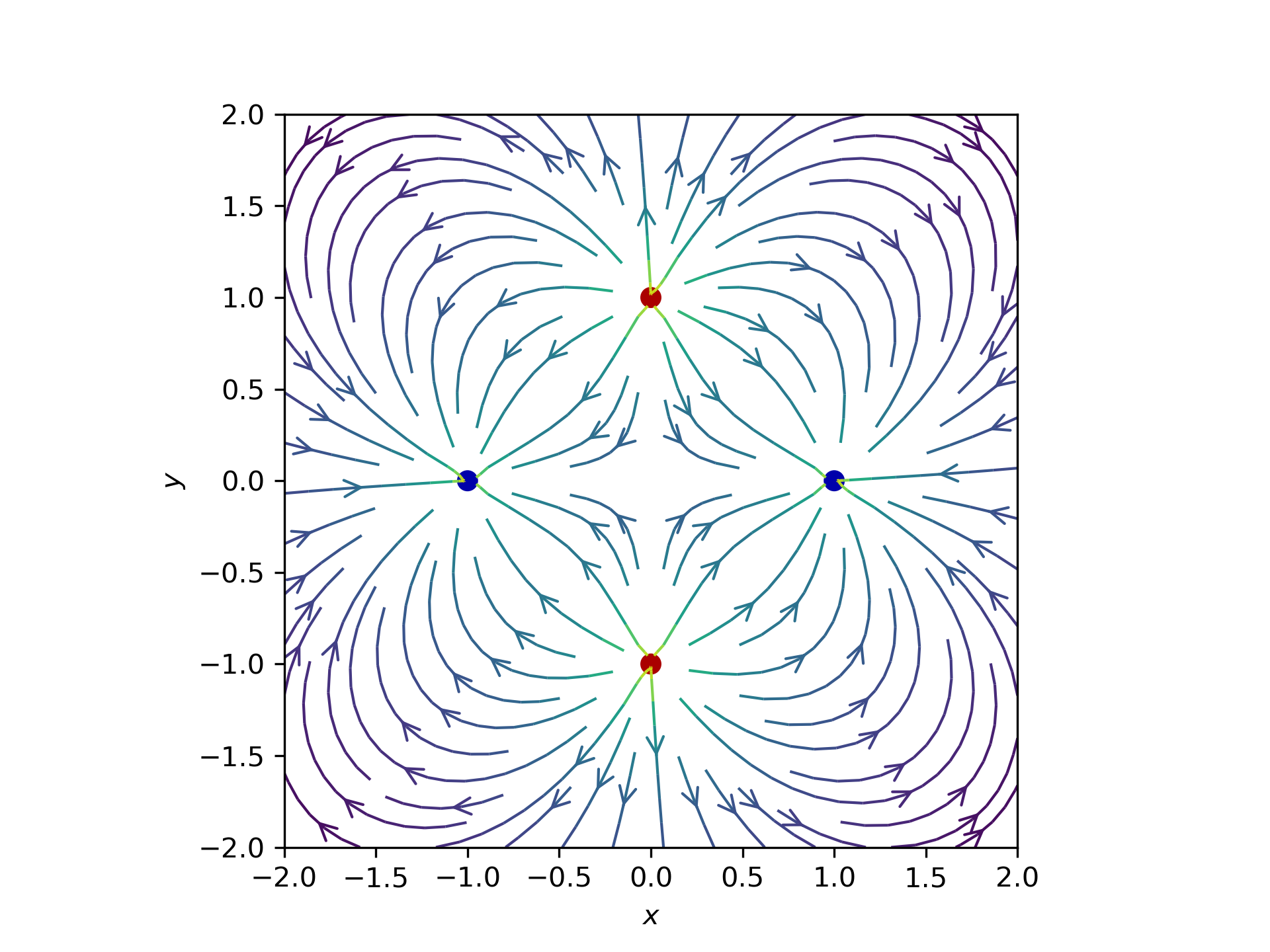
Ottupolo elettrico
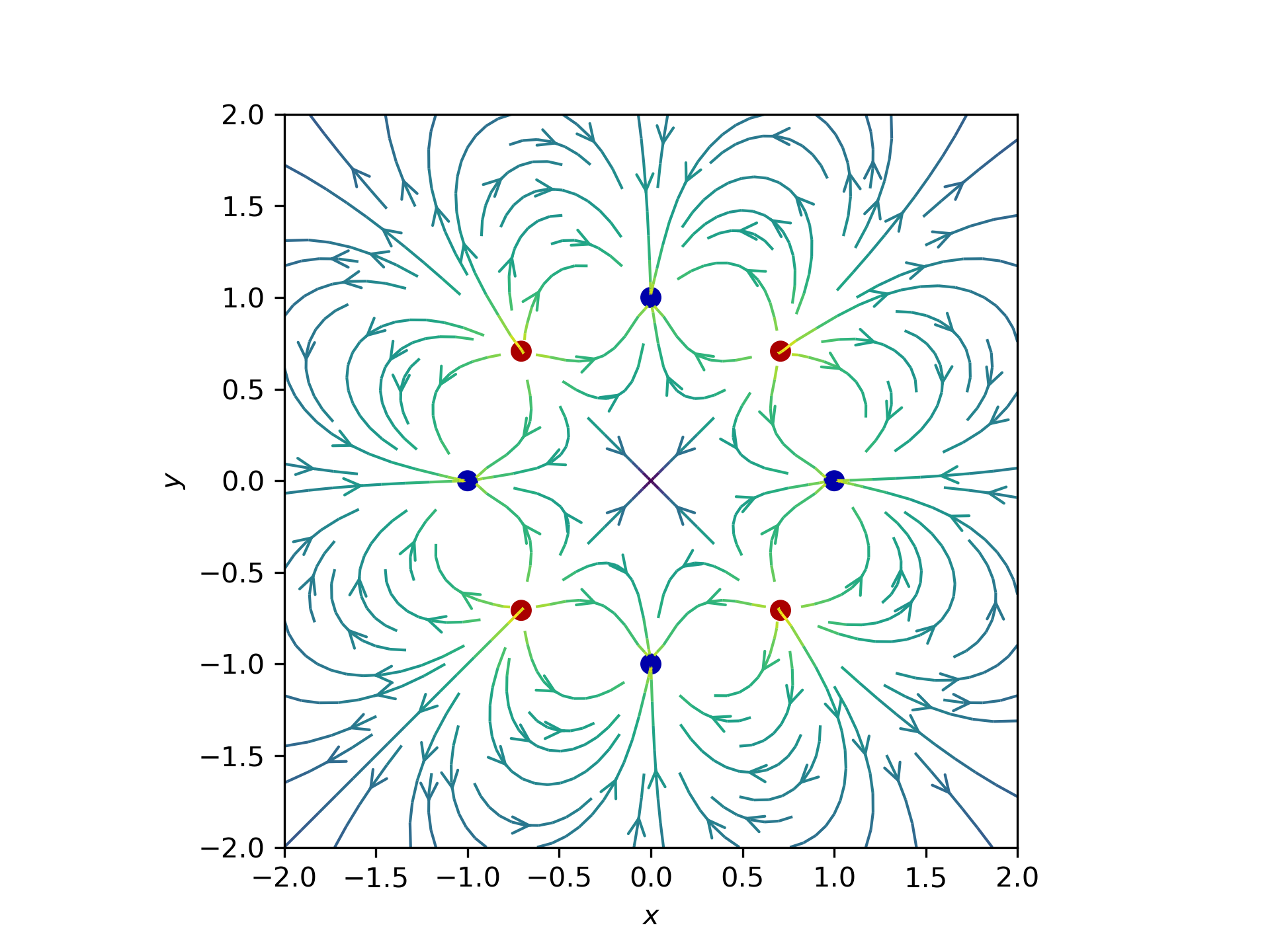
Linee di forza del campo elettrico: 2
Dipolo simmetrico

Dipolo asimmetrico
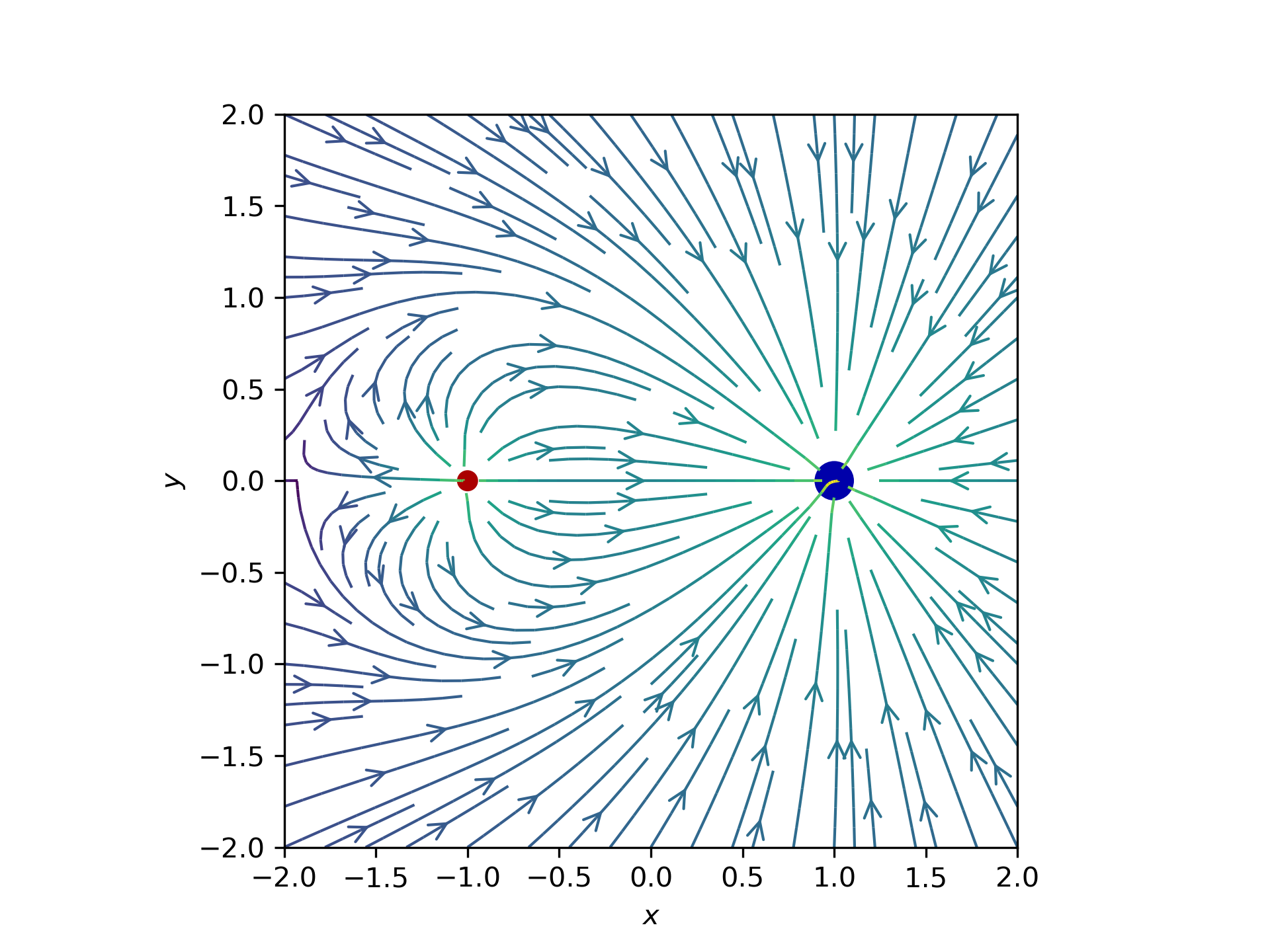
Linee di forza del campo elettrico: 3
Piano carico
Sfere cariche
Moto in un campo elettrico tra due armature cariche
\[ | \vec{E} | \approx costante \]
\[ \vec{a} = \frac{\vec{F}}{m} = \frac{q \vec{E}}{m} \]
Flusso di un campo vettoriale
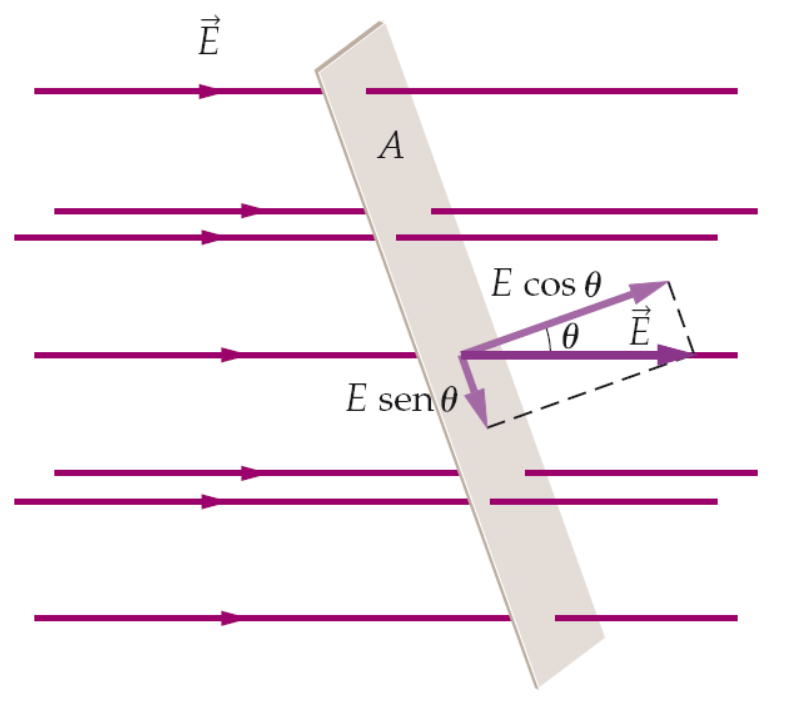
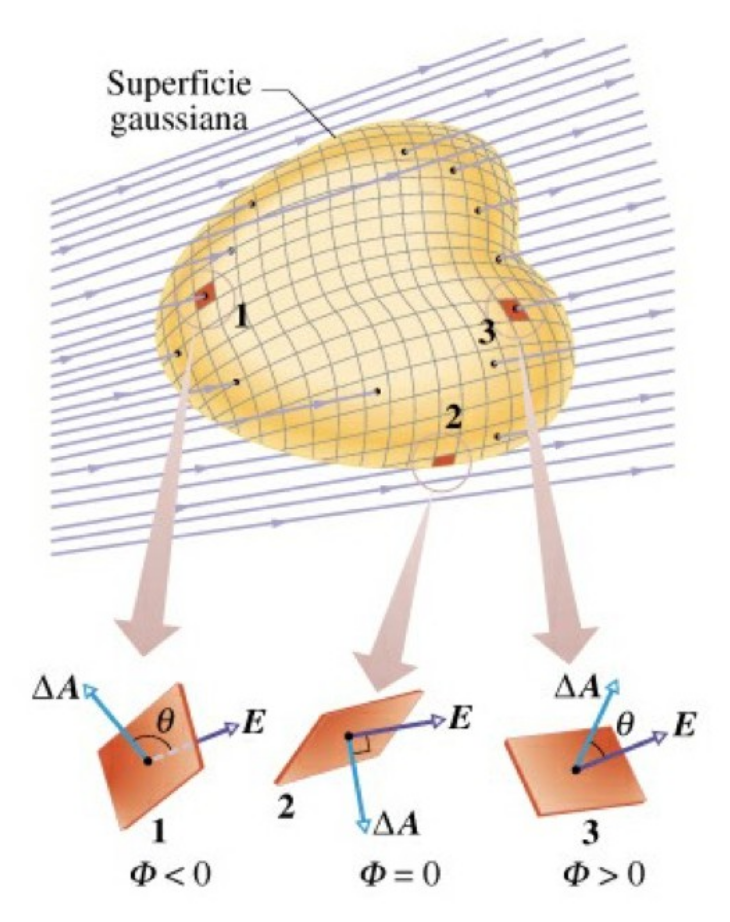
\[ \Phi = \vec{E} \cdot \vec{A} = E \, A \, cos(\theta) \]
\[ \Phi = \sum_{i} \vec{E}_{i} \cdot \Delta \vec{A}_{i} \Rightarrow \Phi = \int_{A} \vec{E} \cdot d\vec{A} \]
Teorema di Gauss
"Il flusso del campo elettrico attraverso una superficie chiusa è proporzionale alla carica racchiusa al suo interno"
\[ \Phi_{E} = \int_{A} \vec{E} \cdot d\vec{A} = \frac{q_{tot}}{\varepsilon_{0}} \]
Esempi di utilizzo del teorema di gauss
Energia potenziale e potenziale elettrostatico
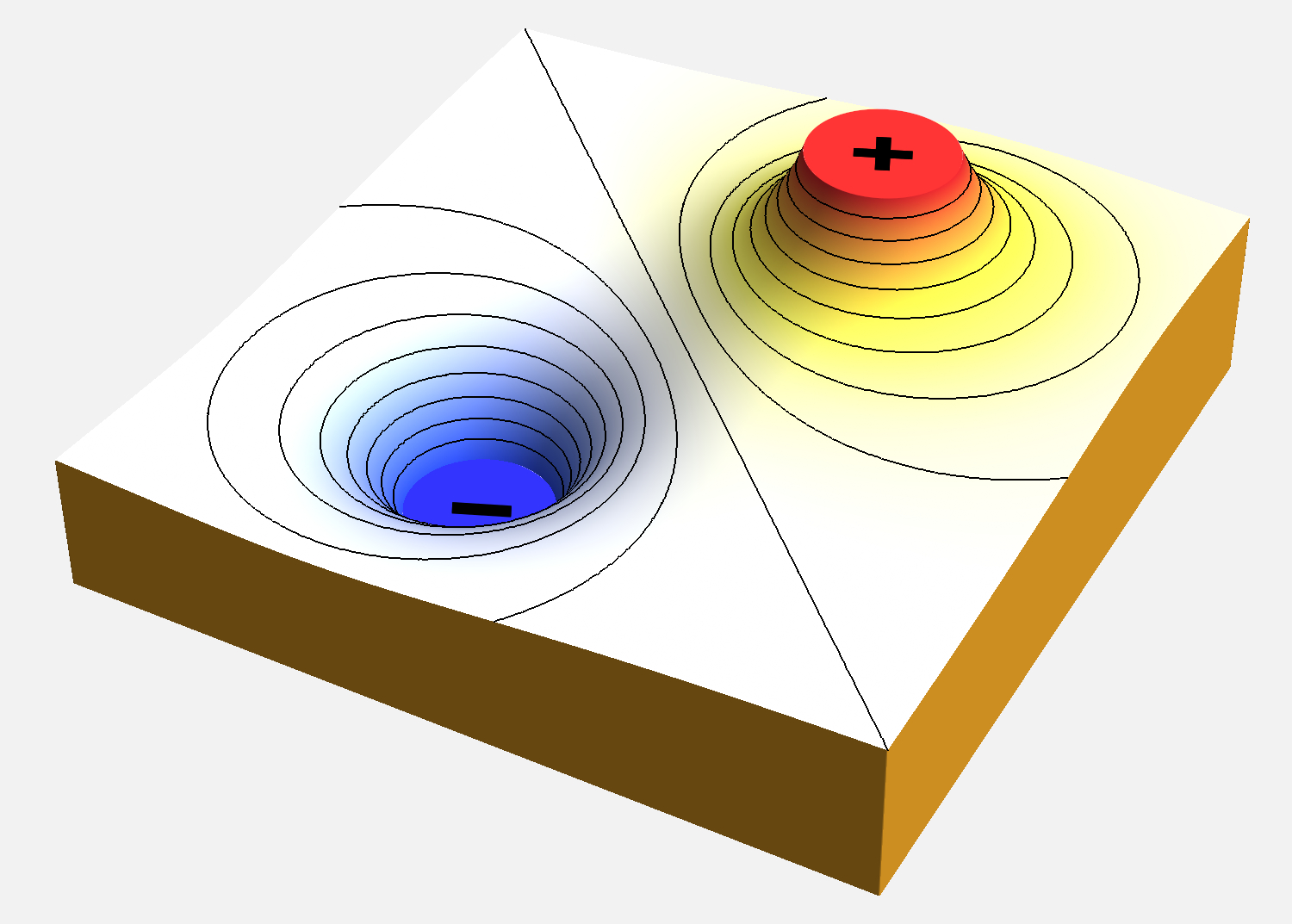
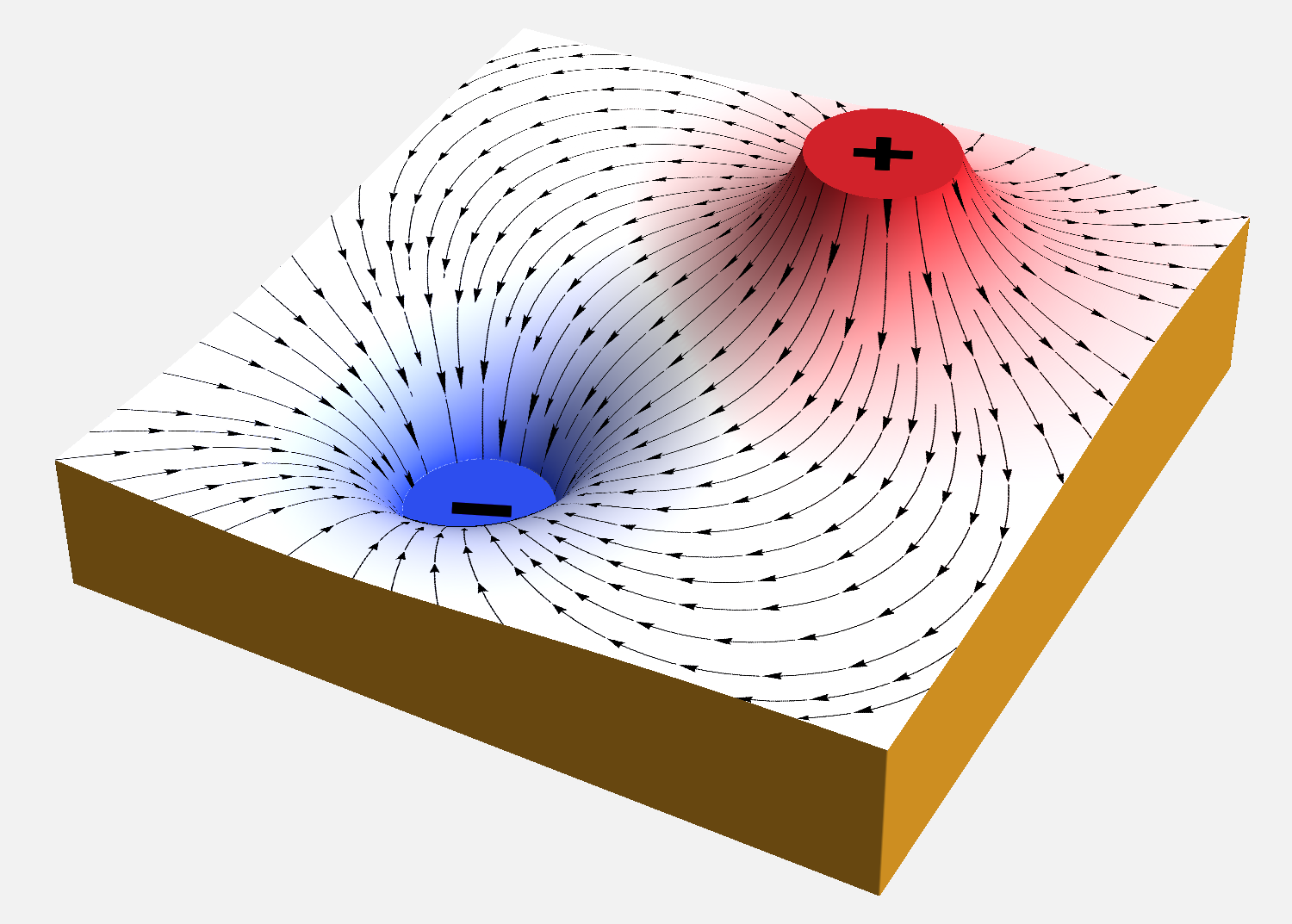
"La forza elettrostatica è una forza conservativa, quindi il suo lavoro può essere espresso tramite una variazione di energia potenziale"
\[ L^{el}_{A \to B} = \int_{A}^{B} \vec{F}_{el} \cdot d \vec{s} = -(U_{e}(B) - U_{e}(A)) = - \Delta U_{e} \]
\[ \frac{L^{el}_{A \to B}}{q} = \int_{A}^{B}\vec{E}_{el} \cdot d \vec{s} = -(V(B) - V(A)) = - \Delta V \]
\[ \Delta U_{e}= q \Delta V \]
\[ U_{e} \to [J] \; \Rightarrow \; V \to \left[ \frac{J}{C} \right] ;\; [Volt] \]
Potenziale di una carica positiva
Potenziale di una carica negativa
Potenziale di una distribuzione di cariche
Una simulazione del campo elettrico
Proprietà dei conduttori carichi
"All'equilibrio, il campo elettrico all'interno di un conduttore carico è nullo. Di conseguenza l'eccesso di cariche presenti è confinato alla superficie."
"All'equilibrio un conduttore è una superficie equipotenziale"
Capacità di un conduttore carico (condensatori)
Ed energia immagazzinata in un conduttore carico
"La capacità mette in relazione la carica accumulata su un conduttore in relazione al suo potenziale"
\[ C = \frac{Q}{V} \; \; \; [F] \]
\[ U_{e} = \frac{1}{2} \frac{Q^{2}}{C} = \frac{1}{2} Q V \]
Condensatori in serie ed in parallelo
Corrente elettrica
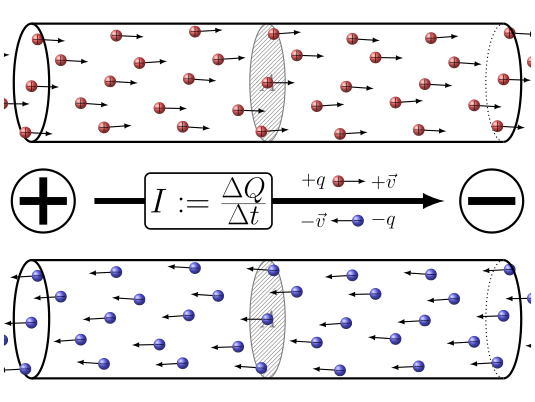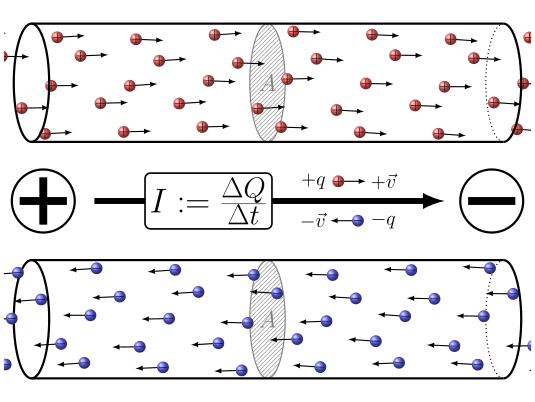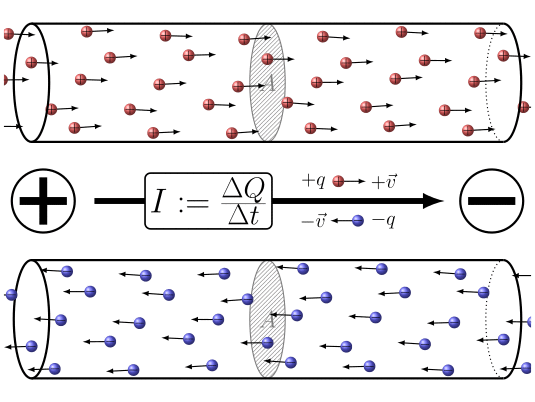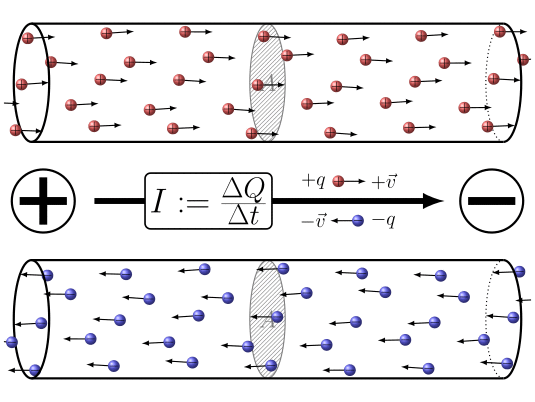
"La corrente elettrica è un moto ordinato di cariche elettriche"
\[ I = \lim_{\Delta t \to 0} \frac{\Delta q}{\Delta t} = \frac{dq}{dt} = Corrente \]
\[ Ampere \, [A] \Rightarrow \left[ \frac{C}{s} \right] \]
Interpretazione microscopica della corrente e densità di corrente elettrica

\[ I = q \,n \, A \, v_{d} \]
- \( q = carica \, del \, portatore \, [C] \)
- \( n = cariche \, libere \, per \, unità \, di \, volume \, [m^{-3}] \)
- \( A = sezione \, del \, conduttore \, [m^{2}] \)
- \( v_{d} = velocità \, di \, deriva \, [m/s]; \, v_{d} \propto \Delta V \)
\[ J = \frac{I}{A} = q \, n \, v_{d} = Densit \grave{a} \, di \, corrente \]
Resistenza, resistività e legge di ohm
\[ V = I \, R \]
\[ R = \rho \frac{L}{A} \]
\( R = resistenza \Rightarrow Ohm \, [\Omega] = \left[ \frac{V}{A} \right] \)
\( \rho = resistività \Rightarrow \left[ \frac{\Omega}{m} \right] \)
Resistenze in parallelo
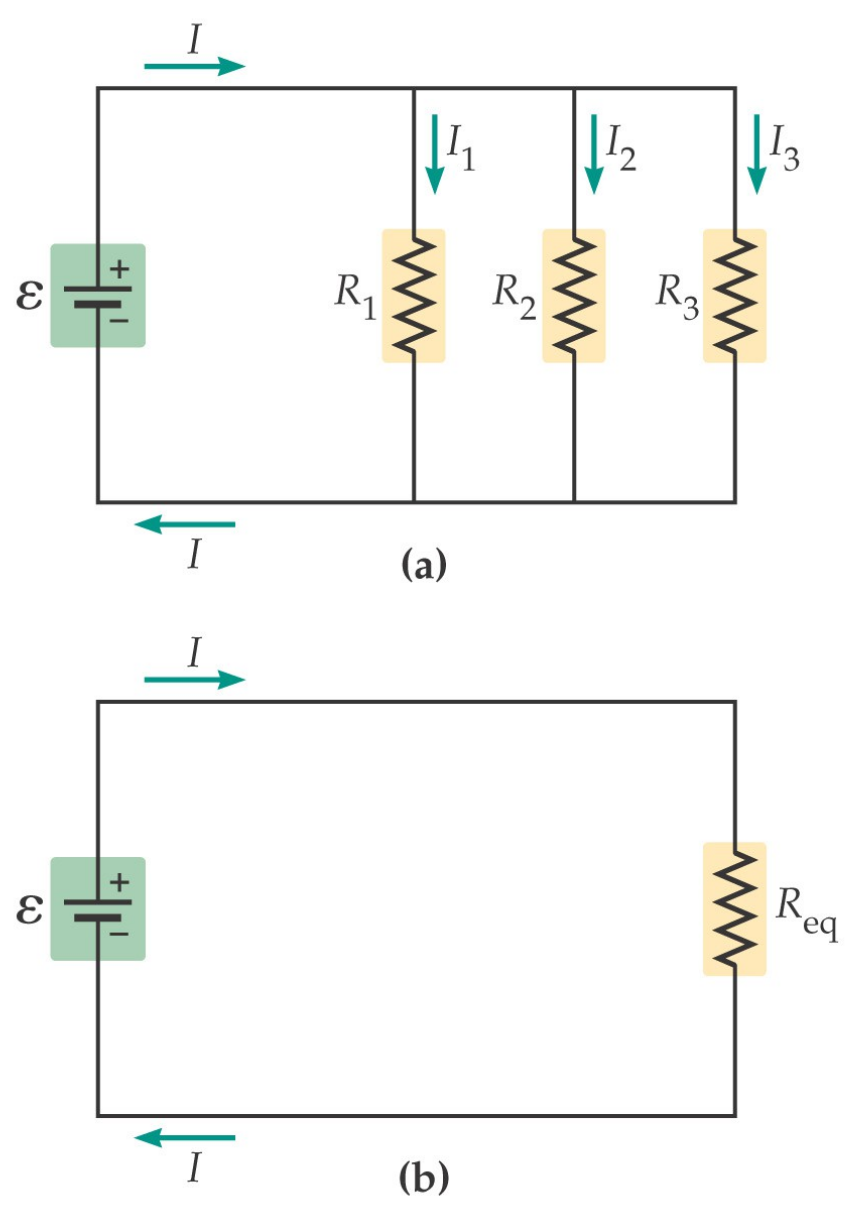
\[ \frac{1}{R_{eq}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} \]
Resistenze in serie
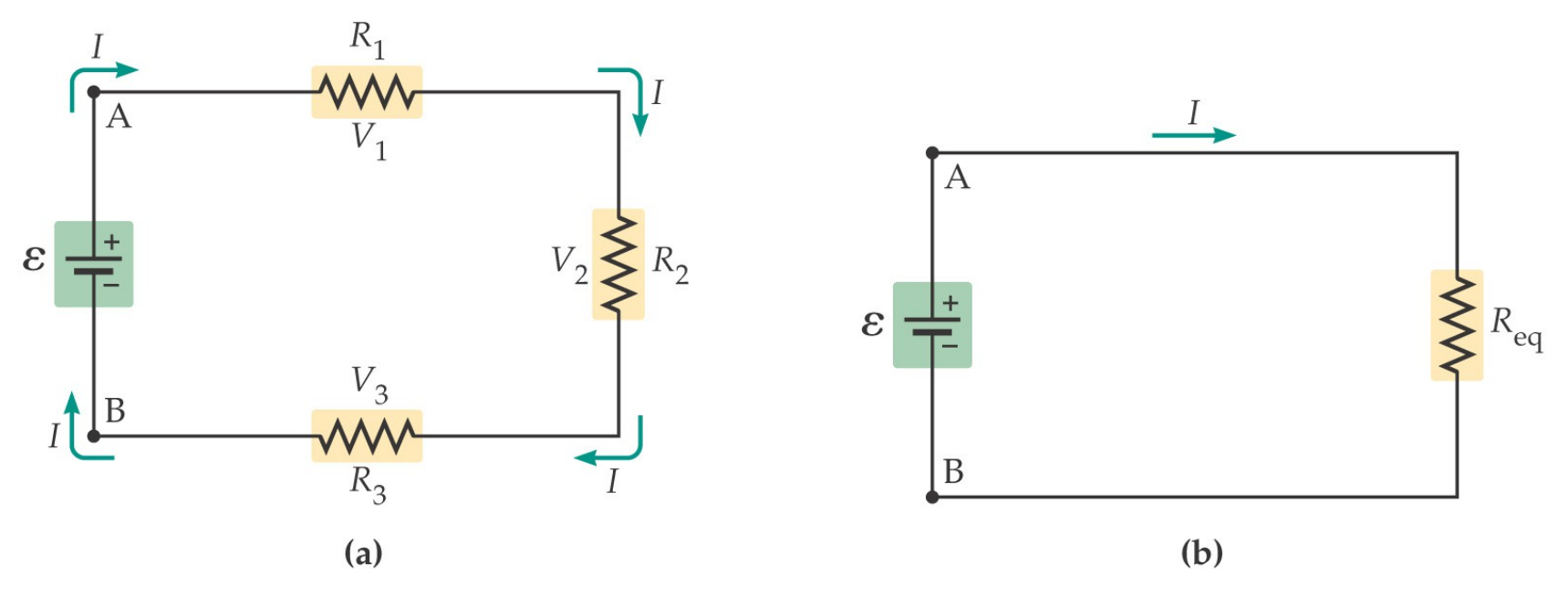
\[ R_{eq} = R_{1} + R_{2} + R_{3} \]